Independent vs Dependent Events

Independent Events

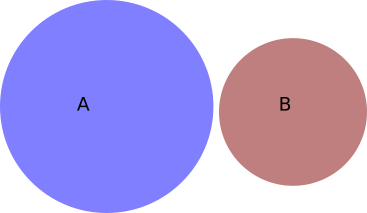
Independent events means that the occurrence of one event does not affect the chance of occurrence of the other event.

The image above represents independent events where the sum of the probabilities of the independent events is,

$$ P(A) + P(B) = 1 $$

Dependent Events

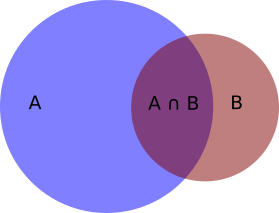
The image above represents dependent events, where the occurrence of one event does affect the chance of occurrence of the other event. Therefore, for dependent events the following holds,

$$ P(A) + P(B) > 1 $$

as there is an overlap where $A$ and $B$ can happen, denoted $P(A \cap B)$.

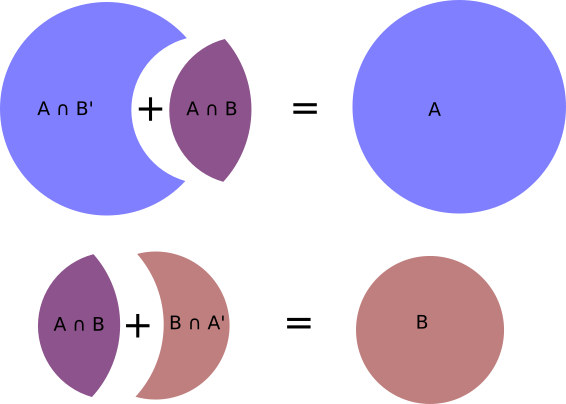
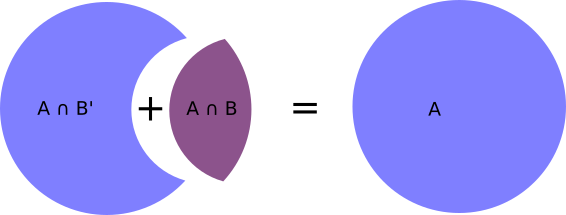
For dependent events, occurrence of A includes two potential cases: The case where A occurs and B does not occur, denoted $A \cap B'$, or the case where A occurs and B occurs as well, denoted $A \cap B$. Therefore,

$$ P(A) = P(A \cap B') + P(A \cap B) $$

Similarly for B,

$$ P(B) = P(B \cap A') + P(A \cap B) $$

As we can see,

$$ P(A) + P(B) = P(A \cap B') + P(A \cap B) + P(B \cap A') + P(A \cap B) = P(A \cap B') + P(B \cap A') + 2 \cdot P(A \cap B) $$

so we are double counting $P(A \cap B)$. To account for this, we need to subtract off $P(A \cap B)$ from the equation above.

$$ P(A) + P(B) - P(A \cap B) = P(A \cap B') + P(B \cap A') + P(A \cap B) = 1 $$

The above can be visualized as

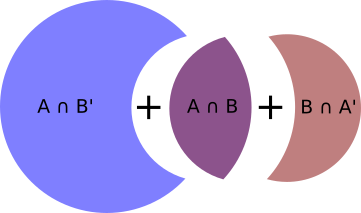
where

Marginal Probabilities

Marginal probabilities are calculated by marginalizing (summing over) all possible states of other variables. This way, we calculate the probability of happening, regardless of the outcome of any other event. $P(A)$ above is a marginal probability because we sum over all possible cases where $A$ can happen.

Dependent Variables

To calculate $P(A)$ for dependent variables, we need to consider two possible states: (1) $A$ happens but $B$ does not $P(A \cap B')$, (2) $A$ happens and $B$ happens $P(A \cap B)$. Note that the sum happens over the possible states of all other events (in this case the sum is over the possible states of $B$).

$$ P(A) = P(A \cap B') + P(A \cap B) $$

Independent Variables

For independent variables, we already have marginal probabilities because $P(A \cap B) = 0$, as by definition the events are independent, so they cannot happen at the same time. Then

$$ P(A) = P(A \cap B') $$

Conditional Probabilities

Conditional probabilities are calculated as the probability of one even happening, given that another event happened. The probability of $A$ happening, given $B$ happened is denoted as $P(A|B)$.

Dependent Variables

Let's say that $B$ has happened already. We can therefore ignore the rest of the plot and just look at

So what is $P(A|B)$? It is the ratio of $P(A,B)$ with $P(B)$.

$$ P(A|B) = \frac{P(A,B)}{P(B)} = \frac{P(A \cap B)}{P(B)} $$

Note that $P(A,B) = P(A \cap B)$, it is just a different notation that is commonly used for the intersection.

Similarly, we can say what is the probability that $B$ happened, given that $A$ happened already, $P(B|A)$. A similar picture to the one above can be drawn, where we only focus on $A$ now.

In this case, $P(B|A)$ is the ratio of $P(A,B)$ with $P(A)$.

$$ P(B|A) = \frac{P(A,B)}{P(A)} = \frac{P(A \cap B)}{P(A)} $$

Independent variables

For independent events, we get $P(A|B) = 0$ and $P(B|A) = 0$. Note again that $P(A,B)=0$ because the events are independent.

Bayes' rule

Rearranging the two equations above, we get

$$ P(A,B) = P(A|B)P(B) \\ P(A,B) = P(B|A)P(A) $$

meaning that

$$ P(A|B)P(B) = P(B|A)P(A) $$

The above makes sense because we end up at the exact same spot (both $A$ and $B$ happening, $A \cap B$) in either of the two cases.

Rearranging again, we get Bayes' rule

$$ P(A|B) = \frac{P(B|A)P(A)}{P(B)} $$